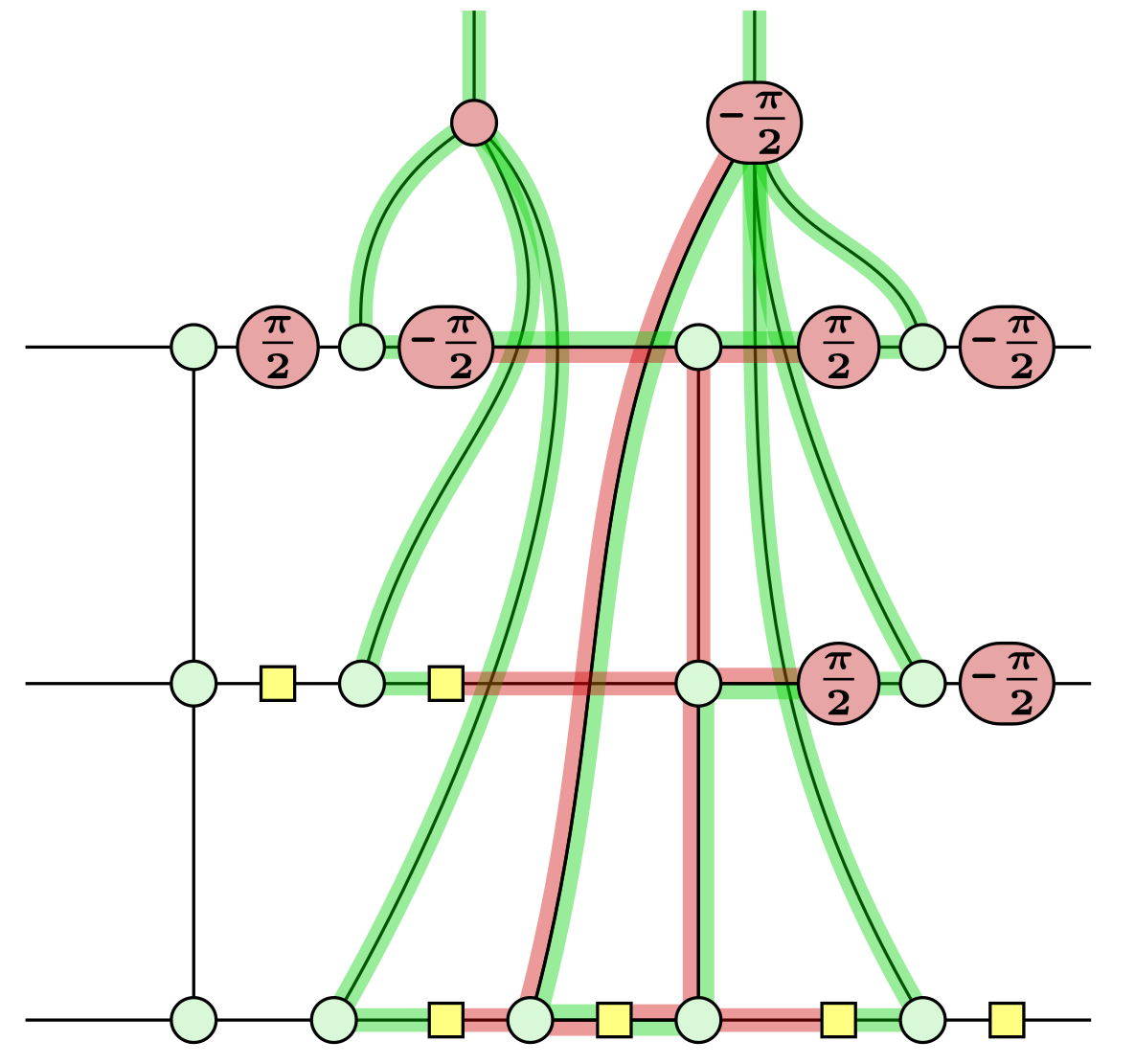
Recently, the novel notion of fault equivalence was introduced to reason about the relationship of noise models on different diagrams. Two diagrams are considered fault-equivalent if every undetectable fault on one diagram has a direct correspondence on the other, both in terms of fault semantics and likelihood. Together with the ZX calculus, a diagrammatic language that is used to reason about quantum computations, fault-equivalent rewrites enable optimisation of a computation without changing its behaviour under noise.
We solidify the framework of fault equivalence by adapting the ZX calculus and providing an axiomatisation that is provably sound and complete for showing fault equivalence on Clifford ZX diagrams. We present useful intermediate notions and tools that extend the formal framework of fault equivalence and reasoning about noise on ZX diagrams in general, and show how they find applications beyond fault equivalence. Furthermore, we provide an implementation that is directly derived from the completeness result as an automated method for showing fault equivalence between diagrams. Through this work, we facilitate fully automatic verification of fault-tolerant implementations of quantum computation specifications under a flexible and formally rigorous notion of noise.
PDF unavailable until further notice.